Answer:
CD = 6.385 units
Explanation:
Given triangle ABC with right angle at C.
And AB = AD + 6 .
Now, consider the triangle ABC.
⇒ cos(∠BAC) =
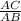 (cosФ = adj/hyp)
(cosФ = adj/hyp)
cos(20) =
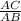 .
.
0.9397 =
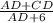
(since AB = AD + 6 and AC = AD + CD)
⇒ 0.9397 AD + 5.6382 = AD + CD
⇒ CD = 0.0603 AD + 5.6382. →→→→→ (1)
⇒ sin(∠BAC) =
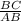 (sinФ = opp/hyp)
(sinФ = opp/hyp)
sin(20) =
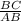 .
.
⇒ BC = AB sin(20) . →→→→→(2)
Now, consider the triangle BCD,
sin(∠BDC) =
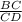
⇒ sin(80) =
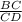
CD =
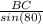
From (2), CD =
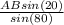 .
.
⇒ CD = AB (0.3473)
⇒ CD = (AD + 6) (0.3473)
⇒ CD = 0.3473 AD + 2.0838 →→→→→→(3)
Now, (1) →→ CD = 0.0603 AD + 5.6382
(3) →→ CD = 0.3473 AD + 2.0838
⇒ 0.0603 AD + 5.6382 = 0.3473 AD + 2.0838
0.287 AD = 3.5544.
⇒ AD = 12.3847
⇒ From (1), CD = 0.0603(12.3847) + 5.6382
⇒ CD = 6.385 units