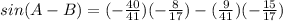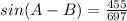Answer:
Part 1)
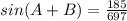
Part 2)
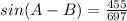
Explanation:
Suppose A is in Quadrant IV and B is in Quadrant III.
If cos(A)=(9/41) and cos(B)=-(8/17)
Part 1) Find sin(A+B)
step 1
Find sin(A)
we know that
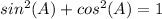
we have

substitute
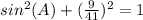
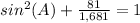
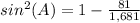
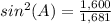
square root both sides
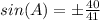
Angle A is in Quadrant IV
so
sine(A) is negative
therefore
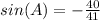
step 2
Find sin(B)
we know that
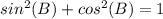
we have
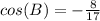
substitute

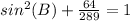
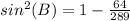
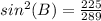
square root both sides
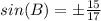
Angle B is in Quadrant III
so
sine(B) is negative
therefore
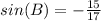
step 3
Find sin(A+B)
we know that
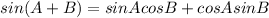
we have
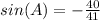

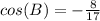
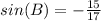
substitute
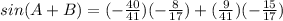
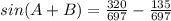
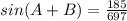
Part 2) Find sin(A-B)
we know that

we have
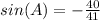

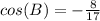
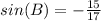
substitute