Question

A person at Mart has decided that they would like to completely fill the ball bin in the toy section with one type of ball. The ball the stock person decided to use had a radius of 2 m. The ball bin is 3.2 meters tall and the opening at the top is 1 meters by 1.5 meters. How many balls should fit inside the bin?

(Hint: Packing spheres in a rectangular prism usually take up 190% of the volume of the spheres

Answer 1

No balls

Explanation:

Given:

The radius of the ball = 2 m

Height of the ball bin = 3.2 metres

Length of of the ball bin = 1 meters

Width of the ball bin = 1.5 metres

To Find:

How many balls should fit inside the bin = ?

Solution:

Step 1: Finding the volume of the ball

The volume of the ball =
`(4)/(3) \pi r^3`

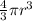
Substituting the value,

=>
`(4)/(3) \pi (2)^3`

=>
`(4)/(3) \pi (8)`

=>
`(100.48)/(3)`

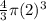
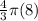
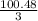
=> 33.49

=>33.5 cubic meters

Step 2: Finding the packing space per ball

=>
`190 \% * \text{volume of one ball}`

=>
`(190)/(100) * 33.5`

=>
`1.9 * 33.5`

=>
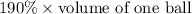
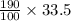
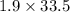
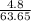`(4.8)/(63.65)` cubic meters

Step 3: Finding the volume of the container

The volume of the rectangular prism (packing box )

=>
`Length * width * height`

=>
`1* 1.5* 3.2`

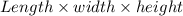
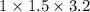
=>4.8 cubic meters

Step 4: Finding the number of ball that can fit in the container

Number of ball =
`\frac{\text{ volume of the container}}{\text{ the packing space per ball}}`

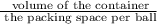
Number of ball =
`(4.8)/(63.65)`

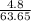
Number of ball = 0.07

No balls can be packed in the bock since the volume of the box is lesser than the packing space required per ball