Question

A company has to buy computers and printers. Each computer, x, costs $585 and each printer, y, costs $385. If the company spends $7,575 and buys a total of 15 machines, how many of each did it buy?

Answer 1

The company bought 9 computers and 6 printers

Solution:

Let "x" be the number of computers bought

Let "y" be the number of printers bought

cost of 1 computer = $ 585

cost of 1 printer = $ 385

The company buys a total of 15 machines

Therefore, we can frame a equation as:

number of computers bought + number of printers bought = 15

x + y = 15 ------ eqn 1

The company spends $7,575

Therefore, we can frame a equation as:

number of computers bought x cost of 1 computer + number of printers bought x cost of 1 printer = 7575

`x * 585 + y * 385 = 7575`

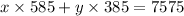
585x + 385y = 7575 ------ eqn 1

Let us solve eqn 1 and eqn 2

From eqn 1,

x = 15 - y --------- eqn 3

Substitute eqn 3 in eqn 2

585(15 - y) + 385y = 7575

8775 - 585y + 385y = 7575

-200y = 7575 - 8775

-200y = -1200

y = 6

Substitute y = 6 in eqn 3

x = 15 - 6

x = 9

Thus the company bought 9 computers and 6 printers