Question

Find the area of a triangle whose vertices are (0,0),(12,0),(2,8).

Answer 1

The area of triangle is 48.

Explanation:

Given:

The vertices of triangle are (0,0),(12,0),(2,8).

Now, to find the area of triangle.

So, the coordinates of triangle are:

`A(x_1,y_1)=(0,0)\:,\:B(x_2,y_2)=(12,0)\:and\:C(x_3,y_3)=(2,8)`.

Now, to get the area of triangle we put formula:

`Area\,of\,triangle\,=\,(1)/(2)\left|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right|`

`Area\,of\,triangle\,=\,(1)/(2)\left|0(0-8)+(12)(8-0)+2(0-0)\right|`

`Area\,of\,triangle\,=\,(1)/(2)\left|0* -8+12* 8+2* 0\right|`

`Area\,of\,triangle\,=\,(1)/(2)\left|0+96+0\right|`

`Area\,of\,triangle\,=\,(1)/(2)\left|96\right|`

`Area\,of\,triangle\,=\,(1)/(2)* 96`

`Area\,of\,triangle\,=\,(96)/(2)`

`Area\,of\,triangle\,=\,48.`

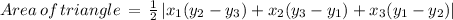
Therefore, the area of triangle is 48.