Question

The altitude of a triangle is a perpendicular segment from the vertex to a line containing the

opposite side. Find H, the length of the altitude of triangle ABC

Answer 1

`H=√(91)`

Explanation:

The altitude falls in the middle of the line.

So, the point at which it falls in the bottom line is the midpoint, so the length of the blue triangle would be 6/2 = 3

So, the blue triangle has length of 3 and height of H and hypotenuse of 10.

Now, we will use Pythagorean Theorem to solve for H. The theorem is:

Leg^2 + Another Leg^2 = Hypotenuse^2

We know one leg of the triangle is 3 and another leg is H and hypotenuse is 10, so we substitute and solve:

`3^2 + H^2 = 10^2\\9+H^2=100\\H^2=100-9\\H^2=91\\H=√(91)`

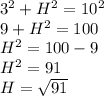
This is the exact answer for H