Question

Intersection point of Y=logx and y=1/2log(x+1)

Answer 1

The intersection is
`((1+√(5))/(2),\log((1+√(5))/(2))`.

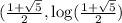The Problem:

What is the intersection point of
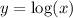`y=\log(x)` and
`y=(1)/(2)\log(x+1)`?

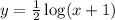Explanation:

To find the intersection of
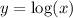`y=\log(x)` and
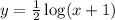`y=(1)/(2)\log(x+1)`, we will need to find when they have a common point; when their
`x` and
`y` are the same.

Let's start with setting the
`y`'s equal to find those
`x`'s for which the
`y`'s are the same.

`\log(x)=(1)/(2)\log(x+1)`

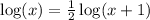
By power rule:

`\log(x)=\log((x+1)^(1)/(2))`

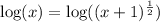
Since
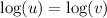`\log(u)=\log(v)` implies
`u=v`:

`x=(x+1)^(1)/(2)`

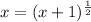
Squaring both sides to get rid of the fraction exponent:

`x^2=x+1`

This is a quadratic equation.

Subtract
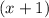`(x+1)` on both sides:

`x^2-(x+1)=0`

`x^2-x-1=0`

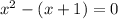
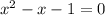
Comparing this to
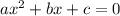`ax^2+bx+c=0` we see the following:

`a=1`

`b=-1`

`c=-1`

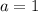
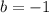
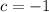
Let's plug them into the quadratic formula:

`x=(-b\pm √(b^2-4ac))/(2a)`

`x=(1 \pm √((-1)^2-4(1)(-1)))/(2(1))`

`x=(1 \pm √(1+4))/(2)`

`x=(1 \pm √(5))/(2)`

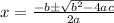
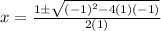
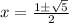
So we have the solutions to the quadratic equation are:

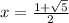`x=(1+√(5))/(2)` or
`x=(1-√(5))/(2)`.

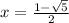The second solution definitely gives at least one of the logarithm equation problems.

Example:
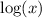`\log(x)` has problems when
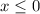`x \le 0` and so the second solution is a problem.

So the
`x` where the equations intersect is at
`x=(1+√(5))/(2)`.

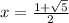Let's find the
`y`-coordinate.

You may use either equation.

I choose
`y=\log(x)`.

`y=\log((1+√(5))/(2))`

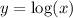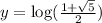
The intersection is
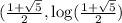`((1+√(5))/(2),\log((1+√(5))/(2))`.