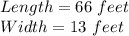Question

If the length of a rectangular field is 12ft less than 6 times it’s width, and perimeter is 158.

Answer 1

Therefore the Dimensions of Rectangular field are

`Length=66\ feet\\Width=13\ feet`

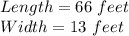
Explanation:

Given:

Let the length of the Rectangular field be ' L '

and Width be 'W'

According to given Condition

`L=6W-12`

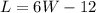
Perimeter = 158 ft

To Find:

L = ?

W = ?

Solution:

Perimeter of Rectangle is given as

`Perimeter=2* L+2* W`

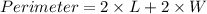
Substitute 'L' and Perimeter we get

`158=2* (6W-12)+2W=12W-24+2W\\\\14W=158+24=182\\\\W=(182)/(14)=13\ feet`

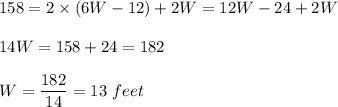
Substitute 'W' in L we get

`L=6* 13-12=66`

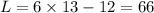
Therefore the Dimensions of Rectangular field are

`Length=66\ feet\\Width=13\ feet`