Question

In rectangle QRST, QS = x2 + 6x, and RT = 8x + 3. Find the length of QS.

Answer 1

The length of QS is 27 units.

Explanation:

In the given rectangle QRST QS and RT are the diagonals. In a triangle, the opposite sides are equal and parallel. This implies that the diagonals of a rectangle are equal.

`QS=RT \ QS=x^2+6x`

`RT=8x+3`

`x^2+6x=8x+3`

`x^2+6x-8x-3=0`

`x^2-2x-3=0`

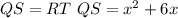
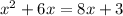
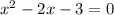
We have obtained a quadratic equation here and solving this gives the possible values of QS.This can be solved using quadratic formula

`x=(-b\pm √((b^2-4ac)))/2a`

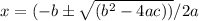
The quadratic equation is of the form
`ax^2+bxl+c=0`

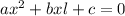
here a=1 b=-2 c=-3

`x=(-b\pm √((b^2-4ac)))/2a`

`x=x=(2 \pm √( (-2^2-4 * 1 * -3)))/(2 * 1)`

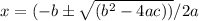
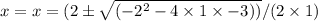
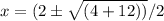`x=(2 \pm √((4+12))) /2` or

`x=(2 \pm √(16))/2 =(2\pm 4)/2 \ \ \ \ x=(2+4)/2=3 \ \ \ \ or  \ \ \ x=(2-4)/2=-1`

putting x=3
`QS=x^2+6x`

`=3^2+6 * 3=9+18=27`

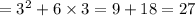
putting x=-1

`QS=(-1)^2+</strong>6 * -1=1-6=-5`

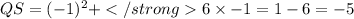
Since a length can have only positive values QS=27 units.