Question

The Segment joining the midpoints of sides PQ and PR (the midsegment) in traingle PQR has length 8x^12x+36. If the length of QR is 4x^2+60x+120, find all possible measures of the midsegment

Answer 1

The possible measures of the midsegment are 32 units and 212 units.

Explanation:

Given:

A triangle PQR with the midsegment made by sides PQ and PR has length equal to
`8x^2+12x+36` and the base length QR opposite to the midsegment is
`4x^2+60x+120`.

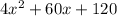From midsegment theorem, we know that, the midsegment is a line parallel to the base opposite to it and half the length of the base length.

Therefore, Midsegment =
`(1)/(2)*` Base length QR

`8x^2+12x+36=(1)/(2)(4x^2+60x+120)\\\\8x^2+12x+36=2x^2+30x+60\\\\(8x^2-2x^2)+(12x-30x)+(36-60)=0\\\\6x^2-18x-24=0\\\\6(x^2-3x-4)=0\\\\x^2-3x-4=0\\\\x^2+x-4x-4=0\\\\x(x+1)-4(x+1)=0\\\\(x+1)(x-4)=0\\\\x=-1\ or\ x=4`

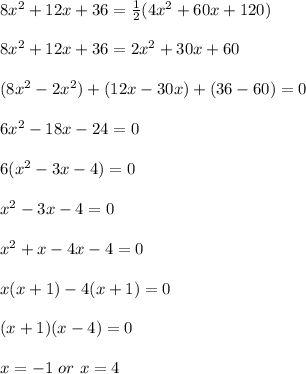
Now, midsegment can be calculated using the values of 'x'.

First, plug in -1 for 'x'. This gives,

`Midsegment=8(-1)^2+12(-1)+36\\\\Midsegment=8* 1-12+36\\\\Midsegment=8-12+36=32\ units`

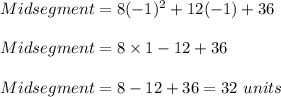
Now, plug in 4 for 'x'. This gives,

`Midsegment=8(4)^2+12(4)+36\\\\Midsegment=8* 16-48+36\\\\Midsegment=128+48+36=212\ units`

Therefore, the possible measures of the midsegment are 32 units and 212 units