Question

Help me please! I really need help on this one! Help would be really appreciated!

Answer 1

Required shingle bundles =
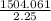`(1504.061)/(2.25)` = 668.5 ≈ 669 bundles.

which costs 669 × 35.99 = 24077.31 dollars.

Explanation:

Let us divide the roof into two parts 1) cuboid and 2) pyramid.

Now, lower part of the roof

1) lateral surface of cuboid.

each surface is a rectangle with length(l) 10.00 m and width(b) 2.32 m

⇒ area = l × b = 10 × 2.32 = 23.2 m²

now, total area of lower part of roof = 4 × 23.2 = 92.8 m²

(4 rectangles / faces)

Now, upper part of the roof.

2) lateral surface of pyramid.

given length of square base of pyramid (l) = 10.00 m

⇒ diagonal length (d) = 10√2 m.

now, given total height of roof = 4.36 m

⇒ height of only upper part (pyramid), h = 4.36 - 2.32 = 2.04 m.

Now, one of the pyramid edges (a) , height of the pyramid (h) and half of the diagonal of the square base (d/2) makes a right angled triangle.

From pythagorus theorem,

(height of pyramid)² + (half-diagonal)² = (length of pyramid edge)²

⇒ h² + (d/2)² = a²

⇒ a² = (2.04)² + (50√2)² = 5004.1616

⇒ a = 70.7400 m.

Length of all the edges of pyramid are same in this case,

length of edge, a = 70.7400 m.

Now, consider one triangular face of pyramid with two of the sides being

a = 70.7400 m and 10.00 m

⇒ area of one face of pyramid =
`√(p(p-a)(p-b)(p-c))`

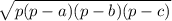
where, p =
`(a+b+c)/(2)`

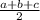
(area of triangle with sides a,b,c is
`√(p(p-a)(p-b)(p-c))`)

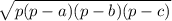Here p =
`(70.7400+70.7400+10)/(2)`.

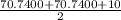p = 75.7400 m.

area of one face =
`√(75.74(75.74-70.74)(75.74-70.74)(75.74-10))`

= 352.815 m²

Total area of upper part of roof = 4 × 352.815 = 1411.261 m²

Now, total area of roof = 92.8 m² + 1411.261 m² = 1504.061 m².

Given that one bundle of shingles cover 2.25 m²

Required shingle bundles =
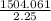`(1504.061)/(2.25)` = 668.5 ≈ 669 bundles.

which costs 669 × 35.99 = 24077.31 dollars.