Question

The answer is (-1,3) but I don't understand how they got that answer. Can someone explain.

Answer 1

The solution is (-1, 3).

Explanation:

Given:

The system of equations are given as:

`y=-x+2\\y=3x+6`

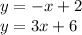
The slope-intercept form of a line is given as:

`y=mx+b`

Where, 'm' is the slope and 'b' is the y-intercept.

For the first equation
`y=-x+2`

`m=-1,b=2`

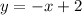
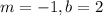
So, the slope is negative and the change of y with x is always equal to 1.

This means that if 'x' changes from 0 to 1, then 'y' will decrease by 1 unit.

Also, the y-intercept is at (0, 2)

Now, marking the point (0, 2) on the graph and then increasing 'x' by 1 unit and decreasing 'y' by 1 unit, we get another point at (1, 1). Then draw a line a passing through these two points. The line is the graph of the first equation.

Similarly, consider the second equation.

`y=3x+6`

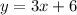
Here,
`m=3,b=6`

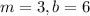
So, we mark the point (0, 6) and then increase 'x' by 1 unit and increase 'y' by 3 units to get the point (1, 9). Draw a line passing through these 2 points.

The graphs are shown below. The point of intersection of both the lines is the required solution. As we can see from the graph, the point of intersection is at (-1. 3).

Therefore, the solution is (-1, 3).