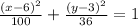Question

Write the equation of a vertical ellipse with a major axis of 20, a minor axis of 12, and a center of (6, 3)

Answer 1

The equation of a vertical ellipse is
`((x-6)^2)/(100) + ((y-3)^2)/(36)   = 1\\`

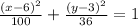
Explanation:

Here, given:

Length of major axis: 20

⇒ 2 a = 20 , or , a = 10

Length of minor axis: 12

⇒ 2 b = 12 , or , b = 6

Also, center (h,k) = (6,3)

Now, STANDARD EQUATION OF ELLIPSE :

`((x-h)^2)/(a^2) + ((y-k)^2)/(b^2)   = 1\\`

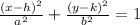
Now, substituting the values, a, b , h and k in above expression, we get:

`((x-6)^2)/(10^2) + ((y-3)^2)/(6^2)   = 1\\`

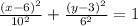
or,
`((x-6)^2)/(100) + ((y-3)^2)/(36)   = 1\\`

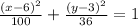
Hence, the equation of a vertical ellipse is
`((x-6)^2)/(100) + ((y-3)^2)/(36)   = 1\\`