The sum of given series is 44
Solution:
Given that we have to find the sum of the series
Given series is:
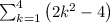
Substitute k = 1 to k = 4 to find the sum of the series
When k = 1:
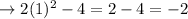
When k = 2:
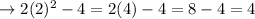
When k = 3:
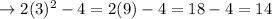
When k = 4:
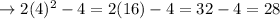
Therefore, the sum of series is given as:
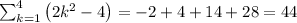
Thus the sum of series is 44