Question

Similar Triangles Question w/ Picture

Please show your work so that I know how to solve it in the future. Thanks!

Answer 1

`EF=(120)/(7)\ ft`

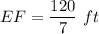
Explanation:

Triangles CEF and CAD are similar right triangles (they have the common angle, so by AA postulate they are similar). Similar triangles have proportional corresponding sides, so

`(EF)/(AD)=(CF)/(CD)\\ \\(EF)/(40)=(CF)/(CD)`

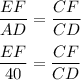
Triangles DEF and DBC are similar right triangles (they have the common angle, so by AA postulate they are similar). Similar triangles have proportional corresponding sides, so

`(EF)/(BC)=(DF)/(DC)\\ \\(EF)/(30)=(CD-CF)/(CD)\\ \\(EF)/(30)=1-(CF)/(CD)`

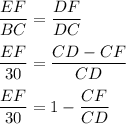
Substitute the fraction
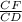`(CF)/(CD)` from the first equality into the second equality:

`(EF)/(30)=1-(EF)/(40)\ [\text{Muliply by 120}]\\ \\4EF=120-3EF\\ \\4EF+3EF=120\\ \\7EF=120\\ \\EF=(120)/(7)=17(1)/(7)\ ft`