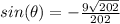Answer:
Part 4)
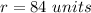
Part 9)
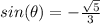
Part 10)
Explanation:
Part 4) A circle has an arc of length 56pi that is intercepted by a central angle of 120 degrees. What is the radius of the circle?
we know that
The circumference of a circle subtends a central angle of 360 degrees
The circumference is equal to

using proportion
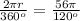
simplify
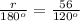
solve for r
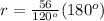
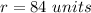
Part 9) Given cos(∅)=-2/3 and ∅ lies in Quadrant III. Find the exact value of sin(∅) in simplified form
Remember the trigonometric identity
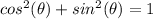
we have
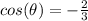
substitute the given value
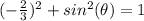
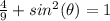
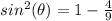
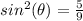
square root both sides

we know that
If ∅ lies in Quadrant III
then
The value of sin(∅) is negative
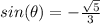
Part 10) The terminal side of ∅ passes through the point (11,-9). What is the exact value of sin(∅) in simplified form?
see the attached figure to better understand the problem
In the right triangle ABC of the figure
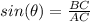
Find the length side AC applying the Pythagorean Theorem
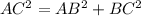
substitute the given values


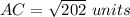
so
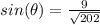
simplify
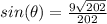
Remember that
The point (11,-9) lies in Quadrant IV
then
The value of sin(∅) is negative
therefore