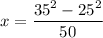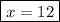Question

Find x. Assume that segments that appear tangent are tangent.

Question 5 options:

47

24

12

19

Answer 1

`x=12`

Explanation:

Since the segment EF appears tangent to the circle, we are assuming that it it is actually tangent.

This assumption gives us a right triangle with base
`x` (because it the radius of the circle), a perpendicular of
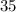`35`, and a hypotenuse of
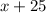`x+25`; therefore, from the Pythagorean theorem we have

`x^2+35^2=(x+25)^2`.

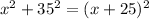Upon expanding the expression on the right side, we get

`x^2+35^2=x^2+50x+25^2`.

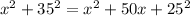Subtract
`x^2` from both sides:

`35^2=50x+25^2`,

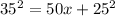and solve for
`x`

`x=(35^2-25^2)/(50)`

`\boxed{x=12}`