Question

Suppose that f(x)=6/x^7 find the following

F’(2)
F’(-1)

Answer 1

f’(2) = -21/128

f’(-1) = -42

Explanation:

We are given a function:

`\displaystyle \large{f(x)=(6)/(x^7)}`

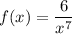
We want to evaluate f’(2) and f’(-1). Keep in mind that f’(x) denotes or means the derivative of f(x). So what we are going to do first is to find the derivative of given function.

Derive the function, there are two ways to derive it, either using power rules or quotient rules. For this, I’ll demonstrate two methods.

Power Rules

If
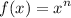`\displaystyle \large{f(x)=x^n}` then
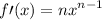`\displaystyle \large{f\prime (x)=nx^(n-1)}` where n is any real numbers.

Since the function is written in a fraction form, we’ll have to convert it to the x^n form using law of exponent.

`\displaystyle \large{f(x)=(6)/(x^7) \to f(x)=6\cdot (1)/(x^7)}`

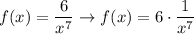
Law of Exponent I

`\displaystyle \large{(1)/(a^n) = a^(-n)}`

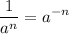
Therefore:

`\displaystyle \large{f(x)=6x^(-7)}`

Then derive the function using power rules:

Property of Differentiation I

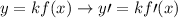`\displaystyle \large{y=kf(x) \to y\prime = kf\prime (x)}` where k is a constant.

`\displaystyle \large{f\prime (x)=6\cdot -7x^(-7-1)}\\\displaystyle \large{f\prime (x)=6\cdot -7x^(-8)}\\\displaystyle \large{f\prime (x)=-42x^(-8)}`

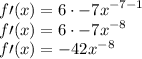
Quotient Rules

`\displaystyle \large{y=(f(x))/(g(x)) \to y\prime = (f\prime (x)g(x)-f(x)g\prime (x))/([g(x)]^2)}`

If f(x) = k or a constant then:

Property of Differentiation II

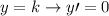`\displaystyle \large{y=k \to y\prime = 0}` for k is a constant.

`\displaystyle \large{y=(k)/(g(x)) \to y\prime = (0\cdot g(x)-kg\prime (x))/([g(x)]^2)}\\\displaystyle \large{y\prime = (-kg\prime (x))/([g(x)]^2)}`

Therefore:

`\displaystyle \large{f\prime (x)=(-6\cdot 7x^(7-1))/([x^7]^2)}\\\displaystyle \large{f\prime (x)=(-42x^6)/(x^(14))}\\\displaystyle \large{f\prime (x)=-42x^(6-14)}\\\displaystyle \large{f\prime (x)=-42x^(-8)}`

Laws of Exponent used above:

`\displaystyle \large{(a^n)^m = a^(nm)}\\\displaystyle \large{(a^n)/(a^m) = a^(n-m)}`

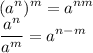
Therefore the derivative of function is:

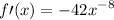`\displaystyle \large{f\prime (x) = -42x^(-8)}` or
`\displaystyle \large{f\prime (x)=-(42)/(x^8)}`

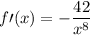
Next is to substitute x = 2 and x = -1 in the derivative.

`\displaystyle \large{f\prime (2)=-(42)/(2^8)}\\\displaystyle \large{f\prime (2) = -(42)/(256)}\\\displaystyle \large{f\prime (2)= -(21)/(128)}`

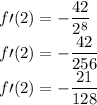
And:

`\displaystyle \large{f\prime (-1)=-(42)/((-1)^8)}\\\displaystyle \large{f\prime (-1) = -(42)/(1)}\\\displaystyle \large{f \prime (-1) = -42}`

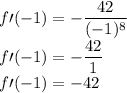
Therefore, f’(2) = -21/128 and f’(-1) = -42.