Hello everyone! can you please help me with this math activity? Help would be very appreciated. The area of a rectangle is 72^(2). State the dimensions of the rectangle with the…

Question

Hello everyone!

can you please help me with this math activity? Help would be very appreciated.


The area of a rectangle is
`72^(2)`. State the dimensions of the rectangle with the least perimeter. Calculate the perimeter.

Answer 1

Dimensions are 6√2 by 6√2 and perimeter = 24√2.

Explanation:

Let p by q gives the dimensions of the rectangle.

So, length = p and width is q.

Now, given that area of the rectangle is, A = pq = 72 ......... (1)

Now, P = 2(p + q) .......... (2) gives the perimeter of the rectangle.

⇒
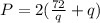`P = 2((72)/(q) + q)` {From equation (1)}

Now, condition for perimeter to be maximum is

`(dP)/(dq) = 0 = 2(-(72)/(q^(2)) + 1 )`

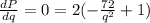
⇒ q² = 72

⇒ q = 6√2

Therefore, from equation (1)
`p = (72)/(6√(2)) = 6√(2)`.

So, the perimeter, P = 2(6√2 + 6√2) = 24√2. {From equation (2)}