Question

You need to fill a basketball with air to play with it. You know that your pump expels air at a velocity of 6 cm/s. You know that the volume flow rate of air being pumped into the basketball is 103 cm^3/s. What is the diameter of your needle?

Answer 1

The diameter of the needle is 4.675 cm.

Step-by-step explanation:

Given:

Volume flow rate is,
`\dot V=103\ cm^3`

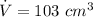
Velocity of air expelled by pump is,
`v=6\ cm/s`

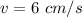
Let the area of the needle be 'A' cm² and the diameter be 'd' cm.

We know that, volume flow rate of the air expelled by pump is given as the product of the needle's area and velocity of air flowing through that area.

Therefore, volume flow rate is given as:

`\dot V=A* v\\\\103=A* 6\\\\6A=103\\\\A=(103)/(6)\ cm^2`

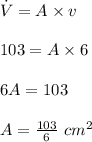
Now, considering the needle to be circular, area of the needle can be written as:

`A=(\pi)/(4)* d^2\\\\(103)/(6)=(\pi)/(4)* d^2\\\\d^2=(103* 4)/(6\pi)\\\\d=\sqrt{(103* 4)/(6\pi)}\\\\d=4.675\ cm`

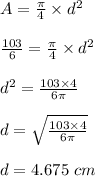
Therefore, the diameter of the needle is 4.675 cm.