Question

Joe is driving west At 60 KM/H and Dave is diving south of 70 KM/H both cars are approaching the intersection of the two roads at what rate is the distance between the cars decreasing when Joe’s car is 0.4 KM and Dave’s is 0.3 KM from the intersection

Answer 1

The distance between the cars is decreasing at 90 Km/h

Explanation:

Instant Rate Of Change

The instant rate of change of a certain magnitude is found by computing its derivative.

The problem requires us to find the rate of change of the distance between Joe and Dave as they approach an intersection. Let y be the distance from Dave to the intersection and x the distance from Joe to the intersection. Since both are moving opposite to the positive reference, their speeds are negative.

Please refer to the figure attached.

The speed of Dave is

`\displaystyle (dy)/(dt)=-70km/h`

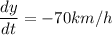
The speed of Joe is

`\displaystyle (dx)/(dt)=-60km/h`

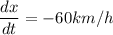
The actual distances to the intersection (origin of coordinates) are

`\displaystyle y=0.3`
`\displaystyle x=0.4`

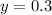
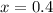
We compute the distance between them by using the Pythagoras's theorem

`\displaystyle h=√(x^2+y^2)`

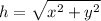
To find the rate of change of the distance, we compute the derivative

`\displaystyle (dh)/(dt)=(2x\ x'+2y\ y')/(2√(x^2+y^2))`

`\displaystyle (dh)/(dt)=(x\ x'+y\ y')/(√(x^2+y^2))`

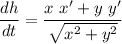
Let's put in numbers:

`\displaystyle (dh)/(dt)=(0.4(-60)+0.3(-70))/(√(0.4^2+0.3^2))`

`\displaystyle (dh)/(dt)=(-24-21)/(0.5)`

`\displaystyle (dh)/(dt)=-90\ km/h`

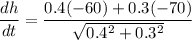
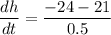
The distance between the cars is decreasing at 90 Km/h