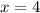Answer:
Part 1)
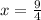
Part 2)
Explanation:
Analize two problems
Part 1) If y varies directly with x, and If y=-8 and x= -3 what’s x when y= 6
we know that
A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
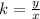 or
or
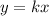
step 1
Find the value of the constant of proportionality k
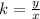
For x=-3, y=-8
substitute the given values
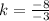
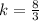
step 2
Find the linear equation
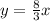
step 3
Find the value of x when y=6
substitute the value of y in the linear equation
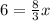
solve for x
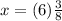
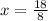
simplify
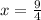
Part 2) If y varies inversely with x, and If y=-8 and x= -3 what’s x when y= 6
we know that
A relationship between two variables, x, and y, represent an inverse variation if it can be expressed in the form
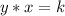 or
or
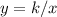
step 1
Find the value of the constant of proportionality k
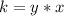
For x=-3, y=-8
substitute the given values
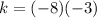
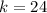
step 2
Find the equation

step 3
Find the value of x when y=6
substitute the value of y in the equation

solve for x