Question

PLEZ HELP

1. This system of equations will be used in all three parts of this question 8x-2y=6 3x+7=4 .

Part 1: Solve the system by graphing. Draw the graphs on paper and indicate their intersection point.

Part 2: Solve the system using the substitution method.

Part 3: Solve the system using the addition method. Show all work here and indicate the solution for the system as an ordered pair.

2. Please provide only one ordered pair (x, y) that will work for both system of inequalities. y>-2x+3 y<4x+1

To earn full credit you must prove your answer by substituting the (x, y) order pair into both inequalities.

Answer 1

Part 1) The solution is the point
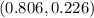`(0.806,0.226)` (see the explanation)

Part 2) The solution is the point
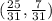`((25)/(31),(7)/(31))` (see the explanation)

Part 3) The solution is the point
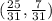`((25)/(31),(7)/(31))` (see the explanation)

Part 4) ordered pair (2,2)

Explanation:

Part 1) Solve the system by graphing

we have

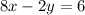`8x-2y=6` ----> equation A

`3x+7y=4` ----> equation B

Solve the system by graphing

Remember that the solution of the system is the intersection point both lines

using a graphing tool

The solution is the point
`(0.806,0.226)`

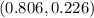
see the attached figure N 1

Part 2) Solve the system using the substitution method

we have

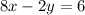`8x-2y=6` ----> equation A

`3x+7y=4` ----> equation B

Isolate the variable y in the equation A

`2y=8x-6`

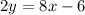
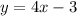`y=4x-3` -----> equation C

Solve the system by substitution

substitute equation C in equation in equation B

`3x+7(4x-3)=4`

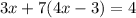
solve for y

`3x+28x-21=4`

`31x=4+21`

`x=(25)/(31)`

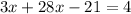
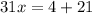
Find the value of y

`y=4((25)/(31))-3`

`y=(100)/(31)-3`

`y=(7)/(31)`

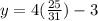
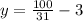
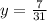
therefore

The solution is the point
`((25)/(31),(7)/(31))`

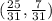
Part 3) Solve the system using the addition method

we have

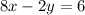`8x-2y=6` ----> equation A

`3x+7y=4` ----> equation B

Multiply equation A by 7 both sides

`7(8x-2y)=7(6)`

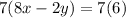
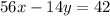`56x-14y=42` -----> equation C

Multiply equation B by 2 both sides

`2(3x+7y)=2(4)`

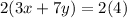
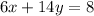`6x+14y=8` -----> equation D

Adds equation C and equation D

`56x-14y=42\\6x+14y=8\\---------\\56x+6x=42+8\\62x=50\\x=(50)/(62)`

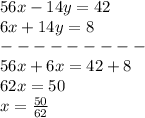
simplify

`x=(25)/(31)`

Find the value of y

substitute the value of x in any equation

equation A

`8((25)/(31))-2y=6`

`(200)/(31)-2y=6`

`2y=(200)/(31)-6`

`y=(100)/(31)-3`

`y=(7)/(31)`

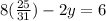
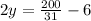
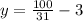
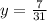
therefore

The solution is the point
`((25)/(31),(7)/(31))`

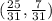
Part 4) Provide only one ordered pair (x, y) that will work for both system of inequalities. y>-2x+3 y<4x+1

we have

`y>-2x+3` ----> inequality A

The solution of the inequality A is the shaded area above the dashed line

The equation of the dashed line A is
`y=-2x+3`

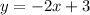
The slope of the dashed line is negative

The y-intercept of the dashed line is (0,3)

The x-intercept of the dashed line is (1.5,0)

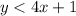`y< 4x+1` ----> inequality B

The solution of the inequality B is the shaded area below the dashed line

The equation of the dashed line B is
`y=4x+1`

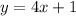
The slope of the dashed line is positive

The y-intercept of the dashed line is (0,1)

The x-intercept of the dashed line is (-0.25,0)

The solution of the system is the shaded area above the dashed line A and below the dashed line B

see the attached figure N 2

Remember that

If a ordered pair is a solution of the system of inequalities, then the ordered pair must lie in the shaded area region of the solution set (makes true both inequalities)

A solution of the system of inequalities is the ordered pair (2,2)

The point lie in the shaded area of the solution set

Substitute the value of x and the value of y of the ordered pair in each inequality

Verify inequality A

For x=2, y=2

`2>-2(2)+3`

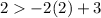
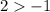`2>-1` ----> is true

so

The ordered pair satisfy inequality A (the ordered pair is a solution of the inequality A)

Verify inequality B

For x=2, y=2

`2< 4(2)+1`

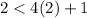
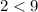`2< 9`----> is true

so

The ordered pair satisfy inequality B (the ordered pair is a solution of the inequality B)

The ordered pair is a solution of the system, because makes true both inequalities