Question

A ball is thrown upward and its height after t seconds can be described by formula f(t)=−10t^2+24t+5.6. Find the maximum height the ball will reach.

Please answer!

Answer 1

The maximum height reached by ball while throwing upward is 20 unit

Explanation:

Given as :

The position of ball moving upward with time t sec is

f(t) = - 10 t² + 24 t + 5.6

Let the maximum height does the ball reach = H unit

Now, For maximum condition

`(\partial f(t))/(\partial t)` = 0

So,
`(\partial ( - 10 t² + 24 t + 5.6 ))/(\partial t)` = 0

Or,
`(\partial (- 10 t^(2)))/(\partial t)` +
`(\partial 2 4 t )/(\partial t)` +
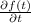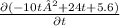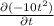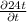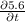`(\partial 5.6)/(\partial t)` = 0

Or, ( - 10 ) × 2 t + 24 + 0 = 0

Or, - 20 t + 24 = 0

Or, 20 t = 24

∴ t =
`(24)/(20)`

i.e t =
`(6)/(5)`

Or, t = 1.2 sec

Again

Double differentiation of the function

i.e
`(\partial^2 (-20t + 24))/(\partial t^2)`

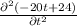
Or, -20 + 0

i.e - 20

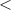∵ - 20
`<` 0

So, The maximum height is gained at t = 1.2 seconds

So, Maximum height at ( t = 1.2 sec) = - 10 t² + 24 t + 5.6

Or, H = - 10 (1.2)² + 24 × 1.2 + 5.6.

Or, H = - 1.44 × 10 + 28.8 + 5.6

Or, H = - 14.4 + 28.8 + 5.6

∴ H = - 14.4 + 34.4

i.e H = 20 unit

So, The maximum height = H = 20 unit

Hence, The maximum height reached by ball while throwing upward is 20 unit . Answer

Answer 2

The maximum height is 20 feet.

Explanation:

The height of the ball after t seconds is given by
`f(t) = -10t^(2) + 24t +5.6`.

For any function, at the maximum point, first order differentiate of the function will be 0, and the second order differentiate will be less than 0.

Now,
`(d f(t))/(dt) = -20t +24`.

As per the given condition,
`-20t +24 = 0\\t = (24)/(20) = (6)/(5)`.

Whatever the value of t is, the second order differentiate of the function is -20, that is
`(d^(2) f(t))/(dt^(2) ) = -20 \leq 0`.

Hence, at t =
`(6)/(5)`, the height of the ball will be maximum.

`f((6)/(5) ) = -10((6)/(5) )^(2) + 24*(6)/(5) + 5.6 = 20`