Question

What’s the answer of a multiplying polynomials (3x-1) to the second power and (x+6) to the second power

Answer 1

`9x^4+102x^3+253x^2-204x+36` is the result of multiplying (3x-1) to the second power and (x+6) to the second power

Solution:

Given that we have to find the result of multiplying polynomials (3x-1) to the second power and (x+6) to the second power

"Second power" means the term is raised to power of 2

Therefore,

We have to multiply
`(3x-1)^2 \text{ and }(x+6)^2`

`\rightarrow (3x-1)^2 * (x+6)^2`

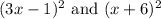
We can use the algebraic identity to expand the above expression

`(a+b)^2 = a^2+2ab+b^2\\\\(a-b)^2=a^2-2ab+b^2`

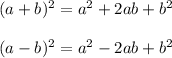
Applying these in above expression, we get

`\rightarrow ((3x)^2-2(3x)(1)+1^2) * (x^2+2(x)(6)+6^2)\\\\\rightarrow (9x^2-6x+1) * (x^2+12x+36)`

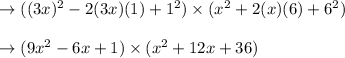
Multiply each term in first bracket with each term in second bracket

`\rightarrow 9x^2(x^2)+(9x^2)(12x)+(9x^2)(36)-6x(x^2)-6x(12x)-6x(36) + x^2+12x+36`

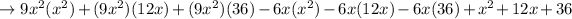
Simplify the above expression

`\rightarrow 9x^4+108x^3+324x^2-6x^3-72x^2-216x+x^2+12x+36`

Combine the like terms

`\rightarrow 9x^4+102x^3+253x^2-204x+36`

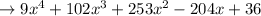
Thus the above expression is the result of multiplying (3x-1) to the second power and (x+6) to the second power