Question

Y varies directly as x and inversely as the square of z. Y=8 when x=25 and z =25 and z =5. Find y when x =3 and z=9

Answer 1

The answer is
`y=(8)/(27)`.

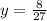Explanation:

Given:

Y varies directly as x and inversely as the square of z.

Y=8 when x=25 and z =5.

Now. to find y when x=3 and z=9.

As given, Y varies directly as x and inversely as the square of z:

Y ∝ x/z².

Now, we multiply by k the constant of variation to convert to an equation:

`y=k* (x)/(z^2)`

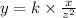
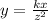`y=(kx)/(z^2)`......(1)

Now, to find
`k` as the direct variation is:

`Y=k(x)/(z^2)`

`Y=k* (x)/(z^2)`

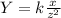
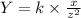
(As, the value of Y = 8, x=25 and z=5.)

`8=k* (25)/(5^2)`

`8=k* (25)/(25)`

`8=k`

`k=8.`

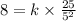
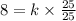
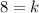
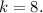
Now, to get the value of y when x=3 and z=9 by putting the value of
`k` in equation (1):

`y=(kx)/(z^2)`

`y=(8* 3)/(9^2)`

`y=(24)/(81)`

`y=(8)/(27)`

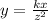
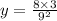
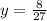
Therefore, the answer is
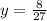`y=(8)/(27)`.

Answer 2

For x =3 , y =
`(24)/(25)`

And for z = 9 , y =
`(200)/(81)`

Explanation:

Given as :

y = 8

x = 25

z = 5

The statements are

(i) y varies directly as x

i.e y ∝ x

Or , y =
`k_1` × x

Now, for y = 8 , and x = 25

Or, 8 =
`k_1` × 25

∴
`k_1` =
`(8)/(25)`

Again

(ii) y varies inversely as the square of z

i.e y ∝
`(1)/(z^(2) )`

Or, y =
`k_2` ×
`(1)/(z^(2) )`

Or, y =
`(k_2)/(z^(2) )`

Now, for y = 8 and z = 5

i.e 8 =
`(k_2)/(5^(2) )`

∴
`k_2` = 8 × 25

Or,
`k_2` = 200

Again

For, for x = 3 and z = 9

∵ y =
`k_1` × x and
`k_1` =
`(8)/(25)`

So, y =
`(8)/(25)` × 3

Or, y =
`(24)/(25)`

Similarly

∵ y =
`(k_2)/(z^(2) )` and
`k_2` = 200

So, y =
`(200)/(9^(2) )`

Or, y =
`(200)/(81)`

Hence, For x =3 , y =
`(24)/(25)`

And for z = 9 , y =
`(200)/(81)` Answer