Question

Which statement is true about the extreme value of the given quadratic equation?

y = -3.2 + 12x – 33
O A. The equation has a maximum value with a y-coordinate of -27.
B.
The equation has a maximum value with a y-coordinate of -21.
0
C.
The equation has a minimum value with a y-coordinate of -21.
0
D.
The equation has a minimum value with a y-coordinate of -27.
Reset
Next

Answer 1

Option B. The equation has a maximum value with a y-coordinate of -21.

Explanation:

The correct quadratic equation is

`y=-3x^(2)+12x-33`

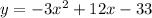
This is a vertical parabola open downward (the leading coefficient is negative)

The vertex represent a maximum

Convert to vertex form

Factor -3

`y=-3(x^(2)-4x)-33`

Complete the square

`y=-3(x^(2)-4x+2^2)-33+12`

`y=-3(x^(2)-4x+4)-21`

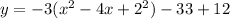
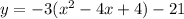
Rewrite as perfect squares

`y=-3(x-2)^(2)-21`

The vertex is the point (2,-21)

therefore

The equation has a maximum value with a y-coordinate of -21