Answer:
The distance of needle cover as it rotate is 0.700688 cm
Explanation:
Given as :
The length of the needle = r = 24 cm
The needle is rotated at angle = Ф = 96°
The distance of needle cover as it rotate = length of arc made = l cm
The radius of arc = length of needle = r cm
Now, According to question
The distance of needle cover as it rotate =
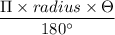
where , π = 3.14
Or, l =
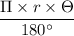
Or, I =

Or, l = 75.36 × 0.533°
∵ 180° = 3.14 radian
So, 0.533° = 0.0092978
So, l = 75.36 × 0.0092978
∴ l = 0.700688 cm
So,The distance of needle cover as it rotate = l = 0.700688 cm
Hence, The distance of needle cover as it rotate is 0.700688 cm Answer