Answer:
The width of the frame is 0.0746 meters
Step-by-step explanation:
We are told that after the frame has been attached to the solar collector, the area that is left exposed is
 . As we see in the figure, the dimensions of this area are
. As we see in the figure, the dimensions of this area are
 and
and
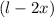
where
 is the width of the frame.
is the width of the frame.
The product of these dimensions must equal the exposed area:
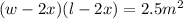
Now since
 and
and
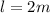 we have:
we have:
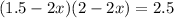
we expand this and solve for x using the quadratic formula:
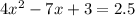
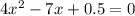
we get two solutions:
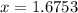

We take the second solution i.e
 , because first one gives a width larger than the dimensions of the solar collector which cannot be possible.
, because first one gives a width larger than the dimensions of the solar collector which cannot be possible.
Thus the width of the frame is 0.0746 meters.