Answer:
The value of
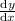 at t = √2 is
at t = √2 is
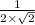 .
.
Explanation:
Given as :
x = t³ - 3 t
y = 3 t²
We have to calculate
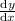 at t = √2
at t = √2
Now,
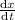 =
=
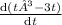
Or,
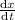 =
=
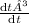 - 3
- 3
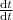
Or,
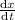 = 3 t² - 3 ......A
= 3 t² - 3 ......A
Again
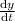 =
=
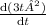
Or,
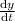 = 3 × 2 t
= 3 × 2 t
Or,
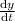 = 6 t ......B
= 6 t ......B
So,
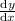 =
=
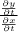
Or,
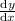 =
=
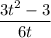
Or,
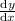 =
=
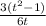
Or,
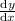 =
=
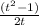
Or,
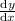 at t = √2
at t = √2
i.e
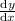 =
=
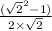
Or,
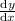 =
=
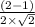
Or,
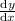 =
=
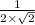
Hence, The value of
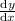 at t = √2 is
at t = √2 is
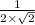 . Answer
. Answer