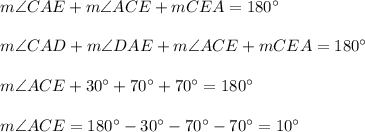Question

CAN SOMEONE PLEASE DO THIS QUICK AND EASY QUESTION PLEASE I NEED HELP LOLOL
CIRCLE THEOREMS

Answer 1

what the guy siad above me is riight

Explanation:

Answer 2

`m\angle AED=70^(\circ)`

`m\angle ACE=x=10^(\circ)`

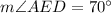
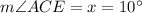
Explanation:

Consider quadrilateral ABDE. This quadrilateral is inscribed in the circle, so the sum of the measures of two opposite angles of quadrilateral is 180°. So,

`m\angle AED+m\angle ABD=180^(\circ)\\ \\m\angle AED+110^(\circ)=180^(\circ)\\ \\m\angle AED=180^(\circ)-110^(\circ)=70^(\circ)`

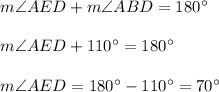
Consider triangle ABD. The sum of the measures of all interior angles in triangle ABD is 180°, so

`m\angle BAD+m\angle ABD+m\ange BDA=180^(\circ)\\ \\m\angle BAD+110^(\circ)+40^(\circ)=180^(\circ)\\ \\m\angle BAD=180^(\circ)-110^(\circ)-40^(\circ)=30^(\circ)`

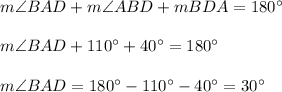
Consider triangle ADE. This triangle is isosceles triangle, because AD = DE. Angles adjacent to the base AE are congruent, so

`m\angle DAE=m\angle AED=70^(\circ)`

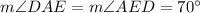
Consider triangle ACE. The sum of the measures of all interior angles in triangle ACE is 180°, so

`m\angle CAE+m\angle ACE+m\ange CEA=180^(\circ)\\ \\m\angle CAD+m\angle DAE+m\angle ACE+m\ange CEA=180^(\circ)\\ \\m\angle ACE+30^(\circ)+70^(\circ)+70^(\circ)=180^(\circ)\\ \\m\angle ACE=180^(\circ)-30^(\circ)-70^(\circ)-70^(\circ)=10^(\circ)`