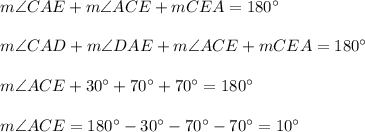Answer:
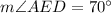
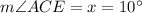
Explanation:
Consider quadrilateral ABDE. This quadrilateral is inscribed in the circle, so the sum of the measures of two opposite angles of quadrilateral is 180°. So,
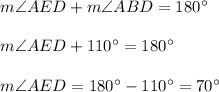
Consider triangle ABD. The sum of the measures of all interior angles in triangle ABD is 180°, so
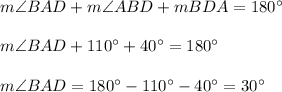
Consider triangle ADE. This triangle is isosceles triangle, because AD = DE. Angles adjacent to the base AE are congruent, so
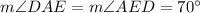
Consider triangle ACE. The sum of the measures of all interior angles in triangle ACE is 180°, so