Answer:
The 19th term of Arithmetic series is - 2.02
Explanation:
Given as :
The product of 5 terms of a GP = 243
The 3rd term of GP is = 10th term of AP
Let The sum of 19th term of AP = x
Now, According to question
∵ nth term of GP is given by
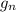 = a×
= a×

where a is the first term and n is nth term and r is the common ratio
So For n = 1
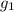 = a×
= a×

Or,
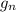 = a×
= a×

i.e
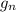 = a × 1
= a × 1
Or,
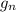 = a
= a
For n = 2
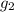 = a×
= a×
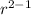
Or,
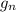 = a×
= a×

i.e
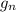 = a × r
= a × r
For n =3
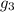 = a×
= a×

Or,
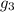 = a×
= a×

i.e
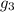 = a × r²
= a × r²
For n =4
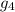 = a×
= a×

Or,
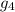 = a×
= a×
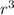
i.e
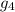 = a × r³
= a × r³
For n =5
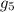 = a×
= a×
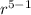
Or,
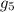 = a×
= a×

i.e
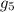 = a ×
= a ×

Now, According to question
product of 5 terms of a GP = 243
So,
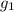 ×
×
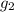 ×
×
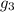 ×
×
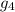 ×
×
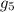 = 243
= 243
Or, a × a r × a r²× a r³× a
 = 243
= 243
Or,
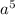 ×
×
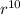 =
=
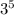
∴, a r² = 3 ............1
Again
3rd term of GP = 10th term of AP
∵ nth term for AP
Tn = a + (n - 1) r , where a is first term and r is common difference
So, 10th term of AP
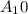 = a + (10 - 1) r
= a + (10 - 1) r
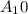 = a + 9 r
= a + 9 r
∵
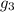 =
=
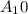
Or, a r² = a + 9 r
Now, from eq 1
3 = a + 9 r
i.e a + 9 r = 3
Or,
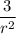 + 9 r = 3
+ 9 r = 3
Or, 3 + 9 r³ = 3 r²
Or, 9 r³ - 3 r² + 3 = 0
Or, r = - 0.59
and a =

i.e a = 8.6
Now, 19th term of AP
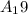 = a + (19 - 1) r
= a + (19 - 1) r
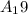 = 8.6 + 18 × (-.59)
= 8.6 + 18 × (-.59)
∴
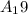 = - 2.02
= - 2.02
So, The 19th term of Arithmetic series = tex]A_19[/tex] = - 2.02
Hence, The 19th term of Arithmetic series is - 2.02 Answer