Question

Which graph represents y=3 sqrt x+2

Answer 1

b

Explanation:

got it on edge 2020

Answer 2

The graph in the attached figure

Explanation:

we have

`y=3√(x+2)`

Remember that the radicand must be greater than or equal to zero

so

`x+2\geq 0`

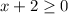
solve for x

subtract 2 both sides

`x\geq -2`

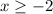
The domain is the interval [-2,∞)

All real number greater than or equal to -2

For x=-2

`y=3√(-2+2)=0`

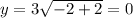
so

The range is the interval [0,∞)

All real number greater than or equal to 0

Find the y-intercept

Remember that the y-intercept is the value of y when the value of x is equal to zero

For x=0

`y=3√(0+2)`

`y=3√(2)`

`y=4.243`

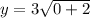
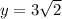
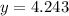
The y-intercept is the point (0,4.243)

therefore

The graph in the attached figure