Answer:
Explanation:
A) the smallest positive integer with exactly 15 factors=144
Because we have
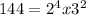
The factors are 1,2,3, 4,6, 8,9, 12, 24, 16, 18,48, 36, 72, 144,
B) We see that 120 is the smallest number with 16 factors.
Because for the smallest number with 16 factors we must have
16 = (3+1)(1+1)(1+1)
Hence one number should be cube and other two prime numbers of degree 1.
Smallest is 2, so we select 2 to have power 3
Number =
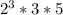 (smallest prime numbers selected)
(smallest prime numbers selected)
No of factors = 4*2^2 = 16
C) First n should be factorised into prime factors starting from possible smallest,
If
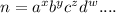 , where a,b,c ... are prime factors in ascending order and x,y,z,w are their exponents
, where a,b,c ... are prime factors in ascending order and x,y,z,w are their exponents
No of factors = (x+1)(y+1) (z+1)(w+1) .......