Answer:
There is sufficient evidence to support the claim that the new balls have bounce heights with a mean different from 92.8292.82 inches, and it appears that the new baseballs are different
Explanation:
Given that in previous tests, baseballs were dropped 24 feet onto a concrete surface, and they bounced an average of 92.82 inches
But new balls showed mean of 92.6 inches with s = 1.72 inches
Sample size = 23
Since sample size is less than 30 and population std deviation is not know we use t test
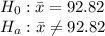
(Two tailed test at 5% significance level)
Mean difference =
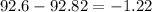
Std error of sample mean = s/sqrt n =

Test statistic t = mean diff/std error = -3.402
df = 23-1 =22
p value = 0.002559
since p value <5% we reject H0
There is sufficient evidence to support the claim that the new balls have bounce heights with a mean different from 92.8292.82 inches, and it appears that the new baseballs are different