Question

4. The average of 5 distinct scores has the same value as the median of the 5 scores. The sum of the 5 scores is 420. What is the sum of the 4 scores that are NOT the median?

Answer 1

336.

Explanation:

We have been given that the average of 5 distinct scores has the same value as the median of the 5 scores. The sum of the 5 scores is 420.

Let us find the average of our given scores.

`\text{Average}=\frac{\text{Sum of all numbers}}{\text{Numbers in a data set}}`

`\text{Average}=(420)/(5)`

`\text{Average}=84`

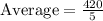
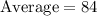
As median of the 5 scores is same as average of 5 scores, therefore, median of the given scores is 84.

We can find the sum of 4 scores that are not median by subtracting median score from total scores.

`\text{Sum of 4 scores that are not median}=420-84`

`\text{Sum of 4 scores that are not median}=336`

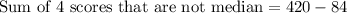
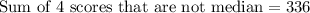
Therefore, the sum of the 4 scores that are not the median is 336.