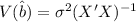Question

an extension of bivariate regression where researchers examine the effects of two or more independent variables on the dependent variable.

Answer 1

See explanation below.

Explanation:

If we assume a linear model with two variables and one intercept the model is given by:

`y_i = \beta_0 + \beta_1 x_(1j) +\beta_2 x_(2j)+ e_i`

The extension of this to a multiple regression modelwith p predictors is:

`y_i = \beta_0 + \sum_(j=1)^p \beta_j x_(ij) +e_i`

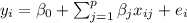
We assume that we have n individuals
`i \in [1,...,n]`

And the distribution for the errors is
`e_i \sim N(0,\sigma^2)`

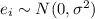
and we can write this model with a design matrix X like this:

`y = Xb + e`

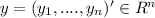`y= (y_1,....,y_n)' \in R^n` a nx1 response vector

`X = [1_n , x_1,....,x_p] \in R^(nx(p+1))` represent the design matrix nx(p+1)

Where
`1_n` is a nx1 vector of ones, and
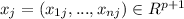`x_j =(x_(1j), ...,x_(nj))\in R^(p+1)` is a (p+1)x1 vector of coeffcients

And
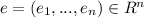`e=(e_1, ...,e_n) \in R^n` is a nx1 error vector

`e \sim N(0_n , \sigma^2 I_n)`

`y|X \sim N (Xb, \sigma^2 I_n)`

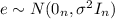
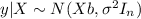
Using ordinary least squares we need to minimize the following quantity:

`min_(b \in R^(p+1)) ||y-Xb||^2`

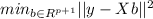
And for this case if we find the best estimator for
`b` we got:

`\hat b= (X'X)^(-1) X' y`

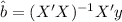
And the fitted values can be written as:

`\hat y = X \hat b`

`\hat y = X(X'X)^(-1)X' y= Hy`

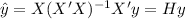
Where
`H= X(X'X)^(-1) X'`

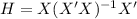
In order to see if any coefficnet is significant we can conduct the following hyppthesis:

Null hypothesis:
`b_j = b_j^*`

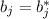
Alternative hypothesis:
`b_j \\eq b_j^*`

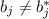
For some j in {0,1,....,p}

We need to use the following statistic:

`Z =(\hat b_j -b_j^*)/(\sigma_(b_j))`

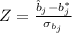
Where
`Z \sim N(0, 1)`

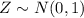
And
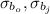`\sigma_(b_o) , \sigma_(b_j)` are square roots of the diagonals of the diagomals of
`V(\hat b) = \sigma^2 (X'X)^(-1)`