Answer:
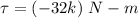
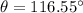
Step-by-step explanation:
Given that.
Force acting on the particle,
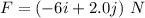
Position of the particle,
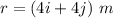
To find,
(a) Torque on the particle about the origin.
(b) The angle between the directions of r and F
Solution,
(a) Torque acting on the particle is a scalar quantity. It is given by the cross product of force and position. It is given by :
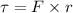

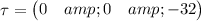
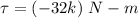
So, the torque on the particle about the origin is (32 N-m).
(b) Magnitude of r,

Magnitude of F,
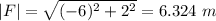
Using dot product formula,
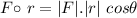
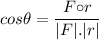
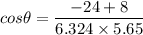
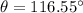
Therefore, this is the required solution.