Question

Given the function
`g(x)=m(-2x+2)^5-n` where m ≠ 0 and n ≠ 0 are constants.

A. Prove that g is monotonic (this means that either g always increases or g always decreases)

B. Show that the x-coordinate(s) of the location(s) of any critical points are independent of m and n

Answer 1

See the explanation.

Explanation:

The given function g(x) is a continuous function, since, for any x we can find a real value of the function.

A.
`(d g(x))/(dx) = 5m(-2x + 2)^(4) * (-2)`.

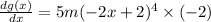Since, m is a constant, which is not equals to 0, the above value of the differentiation of the function, will be negative.

For x = 1, the above value is 0, that is at x = 1, the function has either maximum value, or a minimum value.

B. As per the above information, we have get that for x = 1,
`(d g(x))/(dx) = 0`.

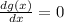Hence, the function's critical point's x coordinate is x = 1.

The x- coordinate of the given point is not dependent on m or n.

Hence, proved.