Question

A gift box has a volume of 450 cubic inches. The width of the box is 4 inches less than the length. The height is twice the width. What is the width in inches of the gift box?

Answer 1

width = 5 in

length = 5+4=9 in

height = 2(5)= 10 in

Explanation:

A gift box has a volume of 450 cubic inches.

Let 'w' be the width of the box

The width of the box is 4 inches less than the length.

`length = w+4`

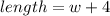
The height is twice the width.

`height = 2 \cdot width`

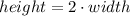
height = 2w

Volume of box = length times width times height

`V=(w+4)(w)(2w)`

`450=(w+4)(w)(2w)`

`450=2w^3+8w^2`

`2w^3+8w^2-450=0`

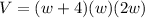
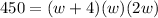
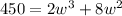
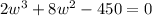
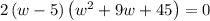
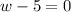
`\quad 2\left(w-5\right)\left(w^2+9w+45\right)=0`

`w-5=0`

w=5

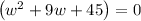`\quad\left(w^2+9w+45\right)=0`, this gives two complex values

so width = 5

length = 5+4=9

height = 2(5)= 10