Question

PLEASE HELP 100 POINTS!! The average monthly temperature changes from month to month. Suppose that, for a given city, we can model the average temperature in a month with the following function.

f(t)= 59 - 26 sin (pi/6 t)


In this equation, f(t) is the average temperature in a month in degrees Fahrenheit, and t is the month of the year (January=1, February=2, ...).


Find the following. If necessary, round to the nearest hundredth.


Minimum average temperature in a month: __ Fahrenheit


Number of cycles of f per month :


Time for one full cycle of f : __ months

Answer 1

Minimum average temperature is 33 °F

Number of cycles of f per month is
`(1)/(12)`

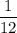
Time for one full cycle is 12 months

Explanation:

`f(t)=59-26 \sin \left((\pi )/(6)t\right)`

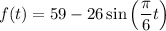
where:

• f(t) = the average temperature a month in °F
• t = month of the year

As
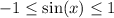`-1\leq \sin (x)\leq 1`, the range of the sine part of the function is:

`-26\leq 26\sin \left((\pi )/(6)t\right)\leq 26`

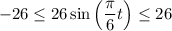
Therefore the minimum temperature will be when

`26\sin \left((\pi )/(6)t\right)=26`

`\implies f(t)=59-26=33 \ \sf \textdegree F`

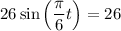
The period of the sine curve is the length of one cycle of the curve. The period is the distance between the peak and the next peak (or trough and the next trough).

To find this algebraically, set the sine part of the function to 26 and solve for t:

`\implies 26\sin \left((\pi )/(6)t\right)=26`

`\implies \sin \left((\pi )/(6)t\right)=1`

`\implies (\pi )/(6)t=(\pi )/(2) \pm 2\pi n`

`\implies t=3 \pm 12n`

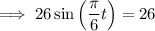
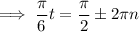
Therefore the period of this function is 12 months.

So the number of cycles of f per month is
`(1)/(12)`

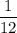
and the time for one full cycle of f is 12 months.