Question

nadia and peter visit a candy store. nidia buys three candy bars and four fruit roll ups for $2.84. peter also buys three candy bars but can only afford one fruit roll up. his purchase cost is $1.79. what is the cost of a candy bar

Answer 1

Cost of 1 candy bar is $ 0.48

Solution:

Let the cost of 1 candy bar be "c"

Let the cost of 1 fruit roll be "f"

Given that, Nadia buys three candy bars and four fruit roll ups for $2.84

Therefore, we can frame a equation as,

three candy bars x cost of 1 candy bar + four fruit roll x cost of 1 fruit roll = 2.84

`3 * c + 4 * f = 2.84`

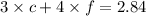
3c + 4f = 2.84 ---------- eqn 1

Peter also buys three candy bars but can only afford one fruit roll up. his purchase cost is $1.79

Therefore, we can frame a equation as,

three candy bars x cost of 1 candy bar + one fruit roll x cost of 1 fruit roll = 1.79

`3 * c + 1 * f = 1.79`

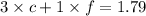
3c + 1f = 1.79 -------- eqn 2

Let us solve eqn 1 and eqn 2

Subtract eqn 2 from eqn 1

3c + 4f - 3c - 1f = 2.84 - 1.79

3f = 1.05

f = 0.35

Substitute f = 0.35 in eqn 1

3c + 4(0.35) = 2.84

3c + 1.4 = 2.84

3c = 2.84 - 1.4

3c = 1.44

c = 0.48

Thus cost of 1 candy bar is $ 0.48