Answer:
The statement Shelly will have $11.2 more in her account than Anne is correct statement .
Explanation:
Given as :
For Anne
The principal deposited in account = $500
The rate of interest = r = 6 % at simple interest
The time period = t = 4 years
Let The amount in account after 4 years =
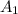
From Simple Interest method
Simple Interest =
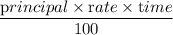
Or, s.i =
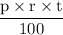
Or, s.i =
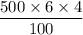
Or, s.i = $120
∵, Amount = Principal + interest
Or,
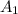 = p + s.i
= p + s.i
Or,
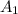 = $500 + $120
= $500 + $120
Or,
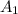 = $620
= $620
So,The amount in account after 4 years =
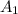 = $620
= $620
Again
For Shelly
The principal deposited in account = $500
The rate of interest = r = 6 % at compounded annually
The time period = t = 4 years
Let The amount in account after 4 years =

From Compound Interest method
Amount = Principal ×
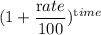
Or, Amount = p ×
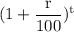
Or,
 = $500 ×
= $500 ×
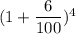
Or,
 = $500 ×
= $500 ×

Or,
 = $500 × 1.2624
= $500 × 1.2624
∴
 = $631.2
= $631.2
So,The amount in account after 4 years =
 = $631.2
= $631.2
Now, Difference between amount in both accounts
i.e Amount into Shelly account - Amount into Anne account = $631.2 - $620
Or, Difference between amount in both accounts = $11.2
∴ It is now clear that amount in credited into Shelly account is $11.2 more
Hence, The statement Shelly will have $11.2 more in her account than Anne is correct statement . Answer