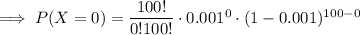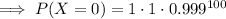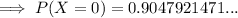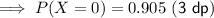Question

1. Solve for X B(100,0.001), for x = 0
a. 0.905
b. 0.917
c. 0.999
d.0.976​

Answer 1

a) 0.905 (3 dp)

Explanation:

Binomial distribution X ~ B(n, p)

where n is the the number of trials and p is the probability of success

Binomial formula:

`P(X=x)=\left(\left\begin{array}{cc}n\\x\end{array}\right) \cdot p^x \cdot (1-p)^(n-x)`

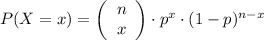
Given: X ~ B(100, 0.001)

Therefore, n = 100 and p = 0.001

Substituting these values into the binomial formula and solving for x = 0:

`\implies P(X=0)=(100!)/(0!100!) \cdot 0.001^0 \cdot (1-0.001)^(100-0)`

`\implies P(X=0)=1 \cdot 1 \cdot 0.999^(100)`

`\implies P(X=0)=0.9047921471...`

`\implies P(X=0)=0.905 \ \sf(3 \ dp)`