Answer:
13
Explanation:
the sum to n terms of a geometric sequence is
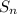 =
=
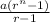
where a is the first term and r the common ratio
here a = 6 , r =
 = 2 and
= 2 and
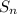 = 49146 , then
= 49146 , then
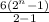 = 49146
= 49146
6(
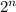 - 1) = 49146 ( divide both sides by 6 )
- 1) = 49146 ( divide both sides by 6 )
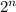 - 1 = 8191 ( add 1 to both sides )
- 1 = 8191 ( add 1 to both sides )
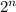 = 8192 ( take log of both sides )
= 8192 ( take log of both sides )
log
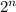 = log 8192 , that is
= log 8192 , that is
n log 2 = log 8192 ( divide both sides by log 2 )
n =
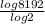 = 13
= 13