Question

Using key terms, create a scenario where you can find a population, a sample, the parameter, the statistic, a variable, and data. Post your scenario and provide a detailed description using the key terms. After reviewing the information, what did you learn about your target population?

Answer 1

See explanation below.

`124 - 2.72 (32)/(√(36))= 109.403`

`124 +2.72 (32)/(√(36))= 138.507`

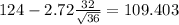
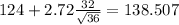
The 99% confidence interval is given by (109.943;138.507) minutes.

We are 99% confident that the true mean for the time to complete the specific difficult question from the test is between 109.943 and 138.507 minutes.

Since the confidence interval contains the value 130 minutes the claim from the researcher makes sense at 99% of confidence.

Explanation:

Previous concepts

Scenario: Consider a test who measure the time to answer a difficult question. The researcher is interested in finding the distribution of the times to answer the specific question. The data is collected from a random sample of 36 participants.

Population: The population can be defined as the people who answer the specific question of the test. The population for this case is all the people who will answer the difficult question from the test.

Sample: A sample is "a randomly selected group of individuals from a population whose characteristics wants to be studied." The sample need to be representative of the population. Our sample for this case would be the 36 individuals that take the test.

Parameter: Population parameter is " a numerical quantity that describes a certain aspect of the population". Our interest on this case is the population mean. On specific the mean time to complete the difficult question from the test.

Statistic: Sample statistic is "an estimated value of the parameter. It is computed using the sample drawn from the population". For our case the statistic is given by the sample mean obtained. And for this study is the avergae obtained from the times to complete the difficult question on the test.

Variable: The variable can be defined as something that is not a constant value. For this case our variable is the time to complete a specific difficult question of a test.

Data: The data in this problem is the time to complete a specific question from the 36 individuals.

After reviewing the information, what did you learn about your target population?

The researcher know that the time to complete the difficult question is about 130 minutes, and he want to test if at 99% of confidence the true mean is around this value.

Define confidence interval and degree of confidence. provide one example of confidence interval and interpret the result?

A confidence interval is "a range of values that’s likely to include a population value with a certain degree of confidence. It is often expressed a % whereby a population means lies between an upper and lower interval".

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

n=36 represent the sample size

The data calculated from the sample are:

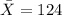`\bar X = 124` represent the sample mean

`s=32` represent the sample standard deviation

In order to find the critical value is important to mention that we don't know about the population standard deviation, so on this case we need to use the t distribution. Since our interval is at 99% of confidence, our significance level would be given by
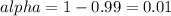`alpha= 1-0.99=0.01` and
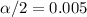`\alpha/2=0.005` . The degrees of freedom are given by:

`df=n-1= 36-1=35`

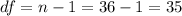
We can find the critical values in excel using the following formulas:

"=T.INV(0.005,35)" for
`t_(\alpha/2)= -2.72`

"=T.INV(1-0.005,35)" for
`t_(1-\alpha/2)= 2.72`

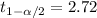
The critical value
`t_c= \pm 2.72`

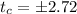
Calculate the margin of error (m)

The margin of error for the sample mean is given by this formula:

`ME= t_c (s)/(√(n))`

`ME= 2.72 (32)/(√(36))= 14.507`

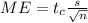
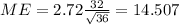
Calculate the confidence interval

The interval for the mean is given by this formula:

`\bar X \pm t_c (s)/(√(n))`

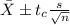
And calculating the limits we got:

`124 - 2.72 (32)/(√(36))= 109.403`

`124 +2.72 (32)/(√(36))= 138.507`

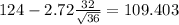
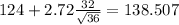
The 99% confidence interval is given by (109.943;138.507) minutes.

We are 99% confident that the true mean for the time to complete the specific difficult question from the test is between 109.943 and 138.507 minutes.

Since the confidence interval contains the value 130 minutes the claim from the researcher makes sense at 99% of confidence.