Question

If a child is randomly selected from Columbus elementary school, what is the probability that the child will be a boy?

(1) If 25 boys are removed from the school, the probability of selecting a boy will be 0.75
(2) There are 35 more boys than there are girls

Answer 1

`G+35 -3G=25`

`2G = 10, G =5`

`B = G+35 = 40`

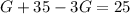
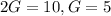
So then the correct option would be:

C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.

Explanation:

Assuming the following options:

A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient.

B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient.

C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.

D. Each statement ALONE is sufficient to answer the question.

E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.

Notation

Let B the event that we select a boy and G the event that we select a girl.

We are interested in find the probability of being boy, on math would be:

`P(B) = (B)/(B+G)`

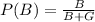
From condition (1) we can do this:

`(B-25)/((B-25)+G) = 0.75 =(3)/(4)`

`4B - 100 = 3B -75 +3G`

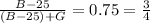
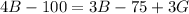
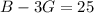`B -3G = 25` (1)

As we can see we have two unknown and we can't solve the system.

Now from condition (2) we can do this:

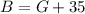`B= G+35` (2)

We see that condition (2) alone is not enouch to solve the problem.

And we need both conditions in order to solve the problem. If we replace equation (2) into equation (1) we got this:

`G+35 -3G=25`

`2G = 10, G =5`

`B = G+35 = 40`

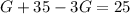
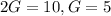
So then the correct option would be:

C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.