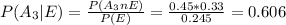Question

According to the most recent adult demographic census of Ohio, 22% of residents are 18 to 29 years old, 45% are between 30 and 49 years old, and 33% are 50 and older. (Age brackets A1, A2, and A3 respectively.) Of Ag4596. those who are in the Al age bracket, 5% use E-Harmony: of those in A2, 19% use E-Harmony; and of those in , Compute the joint probabilities where E an individual uses E-Harmony (It will be helpful to use a probability tree)

P(A1nE)
P(A2nE)
a) What proportion of residents use E-Harmony?
b) You receive a message from an individual using E-Harmony expressing interest. What is the probability the individual is 50 years or older?

Answer 1

a)
`P(E) = P(E|A_1) P(A_1) +P(E|A_2) P(A_2)+ P(E|A_3) P(A_3)`

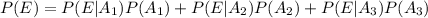
Since we have all the possible values we can replace:

`P(E) = 0.05*0.22 +0.19*0.45+ 0.45*0.33=0.245`

And that would be the proportion of residents who use E-Harmony

We can find the P(A1nE) and P(A2nE) with the following formulas:

`P(A_1 n E)= P(E|A_1) P(A_1) = 0.05*0.22=0.011`

`P(A_2 n E)= P(E|A_2) P(A_2) = 0.19*0.45=0.0855`

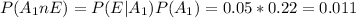
b) For this case we want this probability
`P(A_3 |E)`

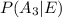
And from the Bayes conditional probability we have this:

`P(A_3 |E) =(P(A_3 n E))/(P(E))=(0.45*0.33)/(0.245)=0.606`

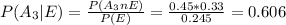
Explanation:

Notation

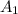`A_1` represent the event resident between 18 and 29 years old

`A_2` represent the event resident between 30 and 49 years old

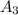`A_3` represent the event resident is >50 yeard old

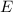`E` represent the event the residen tuse E-Harmony

From the problem we have the following probabilities:

`P(A_1) = 0.22 , P(A_2) = 0.45, P(A_3) = 0.33`

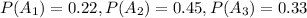
And we have conditional probabilites also given:

`P(E|A_1) = 0.05,  P(E|A_2) = 0.19`

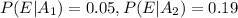
The other probability assumed since the problem is incomplete is:

`P(E|A_3) = 0.45`

Part a

For this case we can use the total probability rule given by:

`P(E) = P(E|A_1) P(A_1) +P(E|A_2) P(A_2)+ P(E|A_3) P(A_3)`

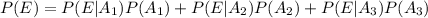
Since we have all the possible values we can replace:

`P(E) = 0.05*0.22 +0.19*0.45+ 0.45*0.33=0.245`

And that would be the proportion of residents who use E-Harmony

We can find the P(A1nE) and P(A2nE) with the following formulas:

`P(A_1 n E)= P(E|A_1) P(A_1) = 0.05*0.22=0.011`

`P(A_2 n E)= P(E|A_2) P(A_2) = 0.19*0.45=0.0855`

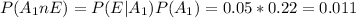
Part b

For this case we want this probability
`P(A_3 |E)`

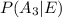
And from the Bayes conditional probability we have this:

`P(A_3 |E) =(P(A_3 n E))/(P(E))=(0.45*0.33)/(0.245)=0.606`