Question

A pharmacist receives a shipment of 22 bottles of a drug and has 3 of the bottles tested. If 5 of the 22 bottles are contaminated, what is the probability that exactly 1 of the tested bottles is contaminated?

Answer 1

There is a 44.16% probability that exactly 1 of the tested bottles is contaminated.

Explanation:

`C_(n,x)` is the number of different combinatios of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

In this problem, we have that:

Total number of combinations:

`C_(22,3) = (22!)/(3!(18)!) = 1540`

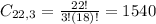
Desired combinations:

It is 1 one 5(contamined) and 2 of 17(non contamined). So:

`C_(5,1)*C_(17,2) = 5*17*8 = 680`

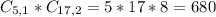
What is the probability that exactly 1 of the tested bottles is contaminated?

`P = (680)/(1540) = 0.4416`

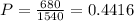
There is a 44.16% probability that exactly 1 of the tested bottles is contaminated.